HI6007 Statistics for business decisions | Australian University Assignment
{`
HI6007 Statistics for business decisions
T2 2021
Final Assignment
Holmes Institute
`}
Assignment Question 1
Briefly discuss the following with relevant examples.
- Population Parameter vs Sample Statistic
- Descriptive Statistics vs Inferential Statistics
- scales of measurement and importance of them in research
ANSWER: ** Answer box will enlarge as you type
Part A
A parameter is a number describing a whole population (e.g., population mean), while a statistic is a number describing a sample (e.g., sample mean).
PART B
Descriptive Statistics
It describes the important characteristics/ properties of the data using the measures the central tendency like mean/ median/mode and the measures of dispersion like range, standard deviation, variance etc.
Inferential Statistics
It is about using data from sample and then making inferences about the larger population from which the sample is drawn. The goal of the inferential statistics is to draw conclusions from a sample and generalize them to the population.
Assignment Question 2
- BB research is a not-for-profit organization in Australia. They seek your help to decide the sampling plan one would choose to collect data for following research. In each case, you are required to explain (a) minimum of two alternative sampling methods, (b) importance of each method for the research and (c) process of sampling with hypothetical data on population and sample.
- Government wants to analysis the peoples’ desire for covid vaccination and willingness to help for government plan for Covid free Australia
- A group of researchers wants to estimate the living standard of people in regional Victoria.
ANSWER:
Government wants to analysis the peoples’ desire for covid vaccination and willingness to help for government plan for Covid free Australia
Then the best sampling plan would be simple random sampling of the citizens. It is a reliable method of obtaining information where every single member of a population is chosen randomly, merely by chance. Each individual has the same probability of being chosen to be a part of a sample.
The alternative sampling plan would be stratified sampling. Stratified random sampling is a method in which the researcher divides the population into smaller groups that don’t overlap but represent the entire population. While sampling, these groups can be organized and then draw a sample from each group separately. Thus the government can divide citizens based on their age group strata or annual income level strata and then pick random samples from each strata
A group of researchers wants to estimate the living standard of people in regional Victoria.
The best sampling plan would be convenience sampling. This method is dependent on the ease of access to subjects such as surveying customers at a mall in Victoria or passers-by on a busy street in Victoria
The alternative sampling plan would be snowball sampling. The government choose to recruit few people living in Australia who would further nominate their known living in Victoria to participate in the survey.
- The following table shows the monthly adverting expenditure and sales revenue of a company. You are required to estimate the covariance and correlation coefficient and explain what do these statistics tell you about the relationship between two variables and advice the company.
|
Sales revenue ($M) |
9.6 |
11.3 |
12.5 |
9.5 |
8.5 |
12 |
11.4 |
12.5 |
13.8 |
14.6 |
|
Advertising expenditure ($000) |
23 |
40 |
55 |
54 |
28 |
25 |
31 |
36 |
88 |
90 |
(Note: Excel calculations are not allowed, and students are required to show all the steps in calculations)
ANSWER:
Lets sales be X and Advertising expenditure be Y
X Values
∑ = 115.7
Mean = 11.57
∑(X - Mx)2 = SSx = 33.761
Y Values
∑ = 470
Mean = 47
∑(Y - My)2 = SSy = 5490
X and Y Combined
N = 10
∑(X - Mx)(Y - My) = 305.2
R Calculation
r = ∑((X - My)(Y - Mx)) / √((SSx)(SSy))
r = 305.2 / √((33.761)(5490)) = 0.7089
The value of R is 0.7089.
This is a moderate positive correlation, which means there is a tendency for high X variable scores go with high Y variable scores (and vice versa).
= 33.911
We find that the covariance coefficient obtained is positive, implying that Sales revenue and Advertising expenditure move together; as one increases (decreases), the other also tends to increase (decrease).
Assignment Question 3
- Sales team of a New Ventures Company is in the process of introducing a new product. As an initial step company conducted a survey of prospective customers. Estimate how large a sample should company take if they want to estimate the proportion of people who will buy the product to within 3%, with 99% confidence.
ANSWER:
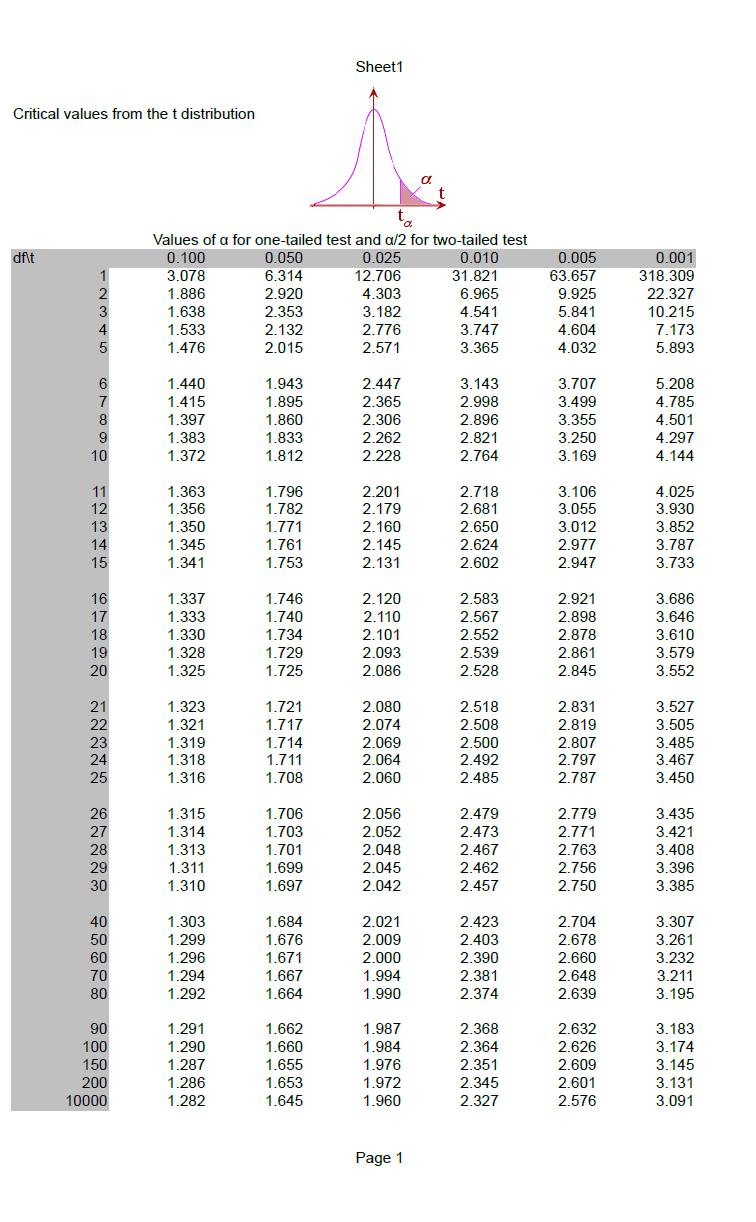
Z = 2.576 at level of significance = 0.01
Margin of error = 3%
Then
N = 0.5*(1-0.5)*(2.576)^2/(0.03)^2 = 1849
- A researcher has taken a random sample of 8 observation from a normal population. Sample mean and standard deviations are 75 and 50 respectively. Using the 6 steps process of hypothesis testing.
- Can he infer at the 10% significance level that the population mean is less than 100?
ANSWER:
- Can he infer at the 10% significance level that the population mean is less than 100 if population standard deviation is 50?
ANSWER:
- Review the answers in (i) and (ii) and explain why the test statistics differed.
ANSWER:
Assignment Question 4
You have been given following data set related to sales of Product X(units) in 3 different locations.
|
Location 1 |
45 |
27 |
39 |
42 |
28 |
|
Location 2 |
30 |
29 |
36 |
21 |
24 |
|
Location 3 |
19 |
25.5 |
27.6 |
31.5 |
34.6 |
You are required to answer following questions.
- State the null and alternative hypothesis for single factor ANOVA to test for any significant difference in sales in three locations. (1 marks)
ANSWER:
Null Hypothesis, H0: µ1 = µ2 = µ3
Alternative Hypothesis, Ha: Not all means are equal
- State the decision rule at 5% significance level. (2 marks)
ANSWER:
Assuming true the null hypothesis at 5% level of significance we will Reject the null hypothesis H0 if the p value is less than 5%.
- Calculate the test statistic. (6 marks)
ANSWER:
The f value is 2.569. The p-value is .117814. The result is not significant at p < .05.
|
location 1 |
location 2 |
location 3 | ||||||
|
45 |
30 |
19 | ||||||
|
27 |
29 |
25.5 | ||||||
|
39 |
36 |
27.6 | ||||||
|
42 |
21 |
31.5 | ||||||
|
28 |
24 |
34.6 | ||||||
|
N |
5 |
5 |
5 | |||||
|
∑X |
181 |
140 |
138.2 | |||||
|
Mean |
36.2 |
28 |
27.64 | |||||
|
∑X2 |
6823 |
4054 |
3962.42 | |||||
|
Std.Dev. |
8.228 |
5.7879 |
5.9702 | |||||
|
Source |
SS |
df |
MS | |||||
|
Between |
234.4053 |
2 |
117.2027 |
F = 2.56943 | ||||
|
Within |
547.372 |
12 |
45.6143 | |||||
|
Total |
781.7773 |
14 | ||||||
- Based on the calculated test statistics, decide whether there are any significant differences between the sales. (2 marks)
ANSWER:
The p-value is 0.1178.
Since the p-value (0.1178) is greater than the significance level (0.05), we fail to reject the null hypothesis. The result is not significant at p < .05.
Therefore, we cannot conclude that there are significant differences between the sales.
Note: No excel ANOVA output allowed. Students need to show all the steps in calculations.
Assignment Question 5
An agronomist undertook an experiment to investigate the factors that potato harvest. In his research, agronomist decided to divide the farm into 30 half hectare plots and apply varies level of fertilizer. Potato was then planted and the harvest at the end of the season was recorded.
|
Fertilizer(Kg) |
Harvest (tons) |
|
210 |
43.5 |
|
220 |
40.0 |
|
230 |
48.0 |
|
240 |
65.0 |
|
250 |
80.0 |
|
260 |
85.0 |
|
270 |
95.0 |
|
280 |
80.0 |
|
290 |
97.3 |
Note: No excel ANOVA output allowed. Students need to show all the steps in calculations.
You are required to;
- Find the simple regression line and interpret the coefficients.
ANSWER:
Let fertilizer(kg) be X
Let harvest ( tons) be Y
Sum of X = 2250
Sum of Y = 633.8
Mean X = 250
Mean Y = 70.4222
Sum of squares (SSX) = 6000
Sum of products (SP) = 4492
Regression Equation = ŷ = bX + a
b = SP/SSX = 4492/6000 = 0.74867; where b is the slope coefficient of fertilizer
a = MY - bMX = 70.42 - (0.75*250) = -116.74444; where a is the constant
ŷ = 0.74867X - 116.74444
this implies that without any fertilizer ( X = 0) there is a harvest of -116.74 which means that infact the crop is all destroyed.
The slope coefficient of fertilizers denotes that for every 1 kg increase in application of fertilizer, the harvest increases by 0.749 tons.
the regression equation for Y is:
ŷ = 0.74867X - 116.74444
- Find the coefficient of determination and interpret its value. (2 marks)
ANSWER:
R= SSXY/sqrt(SSXX*SSYY)
Then R = 0.928
Then coefficient of determination ( R2 ) = 0.928*0.928 = 0.8612
this means that nearly 86.12% of variations in the harvest can be explained by the variation in the application of fertilizers
- Does the model appear to be a useful tool in predicting the potato harvest? If so, predict the harvest when 250KG of fertilizer is applied. If not explain why not. (2 marks)
ANSWER:
Since the coefficient of determination if high, the model is definitely useful in predicting the potato harvest.
Harvest = -116.7444 + 0.74867*(250)
= 70.4306
Hence, predicted value for 250kg fertilizer will be 70.431 tons
Assignment Question 6
ABX Delivery provides the service across all the states in Australia. Marketing manager of this company wants to identify key factors that affect the time to unload a truck. A random sample of 50 deliveries was observed following data were reported.
Time to unload a truck (in minutes),
total number of cartons and
the total weight (in hundreds of Kilograms).
Following tables shows the regression output of the sample data set.
|
SUMMARY OUTPUT | |
|
Regression Statistics | |
|
Multiple R |
0.836420803 |
|
R Square |
0.699599759 |
|
Adjusted R Square |
0.68681677 |
|
Standard Error |
8.823384264 |
|
Observations |
50 |
|
ANOVA | |||||
|
df |
SS |
MS |
F |
Significance F | |
|
Regression |
2 |
8521.530836 |
4260.765 |
54.72897 |
0.000000 |
|
Residual |
47 |
3659.049164 |
77.85211 | ||
|
Total |
49 |
12180.58 |
|
Coefficients |
Standard Error |
t Stat |
P-value | |
|
Intercept |
-13.669 |
7.829028389 |
-1.74599 |
0.087346 |
|
Cartons |
0.5172 |
0.067246763 |
7.691119 |
0.000000 |
|
Weight |
0.2901 |
0.11166803 |
2.597671 |
0.012494 |
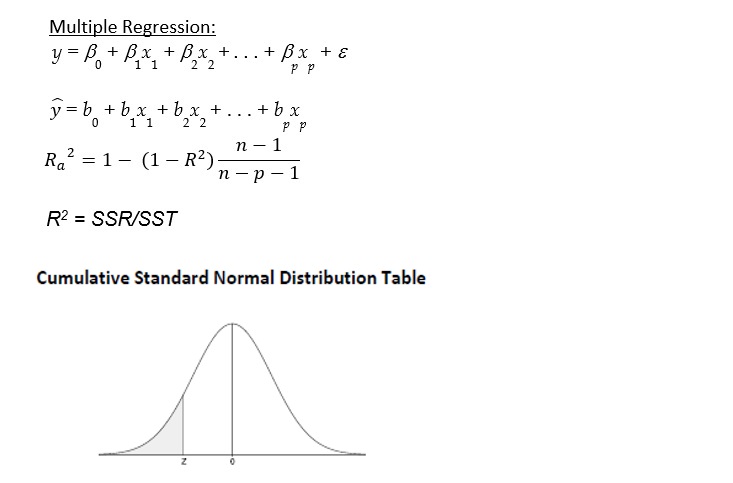
- Determine the multiple regression equation (1 mark)
ANSWER:
TIME TO UNLOAD A TRUCK=-13.669+0.5172*CARTONS+0.2901*WEIGHT
- Develop hypothesis and assess the independent variables significance at 5% level?
(2 marks)
ANSWER:
CASE 1:
For cartons.
Null hypothesis H0: b1 = 0
Alternate hypothesis Ha: b1 ≠ 0
Assuming true the null hypothesis at 95% level of significance we conduct a t test on the regression coefficient of carton (b1). From the above regression table p value for coefficient of cartons is 0.0000; As the p-value is less than 0.05, the null hypothesis is rejected at 5% level of significance and hence it can be concluded that the independent variable CARTONS is significant at 5% level of significance.
CASE 2
For Weight
Null hypothesis H0: b2 = 0
Alternate hypothesis Ha: b2 ≠ 0
Assuming true the null hypothesis at 95% level of significance we conduct a t test on the regression coefficient of weight (b2).The p-value is obtained from the table as 0.012494; As the p-value is less than 0.05, the null hypothesis is rejected at 5% level of significance and hence it can be concluded that the independent variable weight is significant at 5% level of significance.
- How well does the model fit the data? (2 marks)
ANSWER:
The value of R2 is obtained as 0.699599759; It can be interpreted that 69.96% of all the variance of the dependent variable can be explained by the chosen independent variables. Thus, the model fit is good.
- Propose minimum of 2 new explanatory variables to the model and discuss the implication of OLS assumptions in regression analysis. (2 marks)
ANSWER:
We can think of adding two new explanatory variables that can affect unloading time such as (i) Number of manpower involved in unloading the truck and (ii) Total weight of the manpower involved in unloading the truck.
With the addition of these two new variables, there can be following implications of the OLS models that There can be multicollinearity. Multicollinearity generally occurs when there are high correlations between two or more predictor variables.
FORMULA SHEET